모든 사물이 가지고 있는 여러 가지 입체적인 모양 속에는 다양한 2차원적인 모양들이 있습니다. 이 중에 대표적인 모양 중 하나인 삼각형은 표지판, 샌드위치, 고깔모자 등 우리 주변에서 쉽게 찾아볼 수 있습니다. 이번 시간에는 터틀 로봇의 블록 코딩을 이용하여 다양한 삼각형을 그리고 이들의 특징을 이해하며 다양한 삼각형을 배워보고자 합니다.
정삼각형과 이등변 삼각형, 직각삼각형, 예각삼각형과 둔각삼각형을 이해하고 구분할 수 있으며 이들 삼각형의 특징을 알 수 있다.
터틀 로봇에 문제해결 과정을 단계별로 블록코딩하여 삼각형을 그릴 수 있다.
| 컴퓨팅 사고력 |
자료수집 | 자료분석 | 자료표현 | 문제분해 | 추상화 | 알고리즘 | 자동화 |
|---|---|---|---|---|---|---|---|
| ○ | ○ |
[9수학02-01] 삼각형, 사각형, 원의 구성 요소를 이해한다.
[9수학02-02] 여러 가지 삼각형, 사각형을 구별한다.
[9수학02-03] 여러 가지 방법으로 삼각형, 사각형, 원을 만든다.
삼각형의 특징에 대해 알기
정삼각형, 이등변삼각형, 직각삼각형에 대해 알기
예각삼각형, 둔각삼각형에 대해 알기
정삼각형 그리기
이등변삼각형 그리기
직각삼각형 그리기
예각삼각형 그리기
둔각삼각형 그리기
블록 코딩할 때 ‘앞으로 가기’블록과 ‘제자리 돌기’ 블록의 수를 인식할 수 있도록 지도하고 각의 개념은 지도하지 않는다.
터틀 로봇의 블록 코딩 참고 자료
나랑 놀자! 소프트웨어(발달장애학생용) : http://www.nise.go.kr/sedu/pe/pe3/page4_04.html
터틀 로봇의 블루투스 연결하기(동영상) : https://youtu.be/yj4UCjmVRgI?list=PLIrcvBToDsdrUPSDI2Shm-QdkNLTlrXnQ
【학습목표】
1. 정삼각형과 이등변삼각형, 직각삼각형, 예각삼각형과 둔각삼각형을 이해하고 구분할 수 있으며 이들 삼각형의 특징을 알 수 있다.
2. 터틀 로봇에 문제해결 과정을 단계별로 블록코딩하여 삼각형을 그릴 수 있다.
민지는 어제 삼각형으로만 만들어진 나라에 가는 꿈을 꿨어요. ‘사람들도 삼각형, 집도 삼각형, 모두 삼각형이네.’ 너무나도 신기했어요. ‘내가 알고 있는 이런 삼각형 말고 다른 모양의 삼각형도 있을까?’민지는 너무 궁금했어요. 그래서 오늘 삼각형에 관하여 알아보려고 해요. 여러분도 삼각형에 관하여 알아보고 다양한 삼각형을 터틀 로봇과 함께 그려보도록 할까요?

1. 삼각형의 특징에 대해 알기
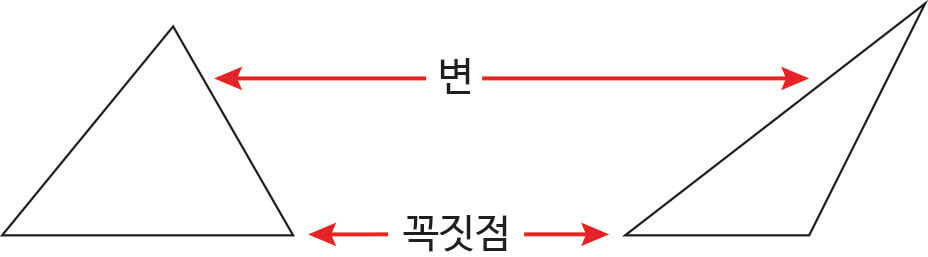
삼각형은 세 선분으로 둘러싸인 도형을 말하는데 삼각형의 곧은 선을 변이라고 하고 두 곧은 선이 만나는 점을 꼭짓점이라고 합니다.
삼각형은 변 3개, 꼭짓점 3개를 가지고 있습니다.
2-1. 정삼각형에 대해 알기
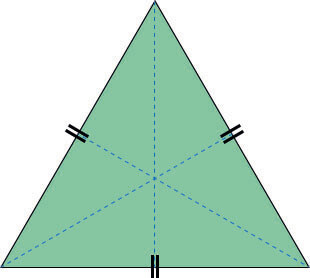
세 변의 길이가 같은 삼각형을 정삼각형이라고 합니다.
2-2. 이등변 삼각형에 대해 알기
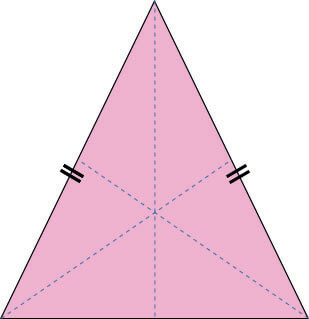
두 변의 길이가 같은 삼각형을 이등변삼각형이라고 합니다.
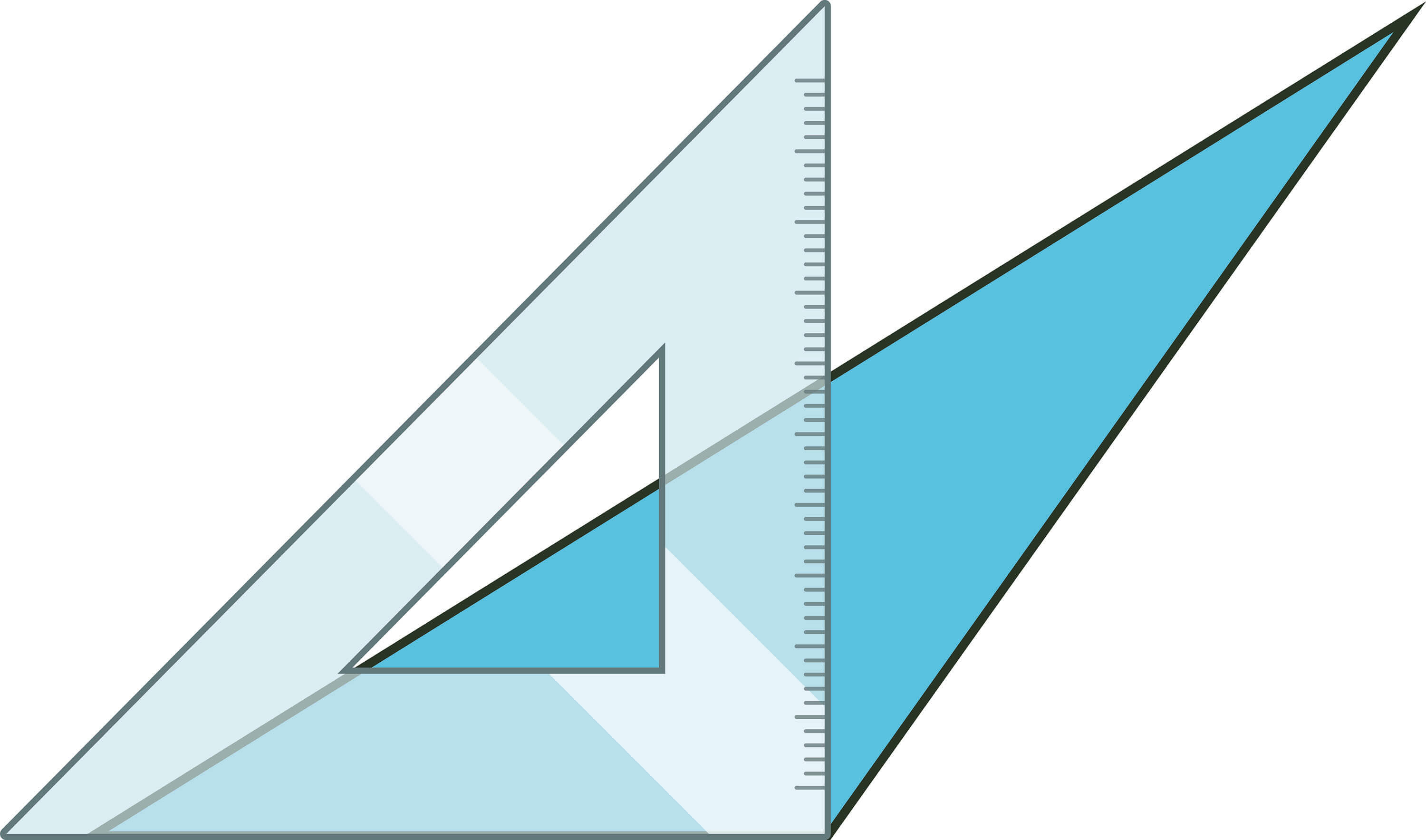
2-3. 직각삼각형에 대해 알기
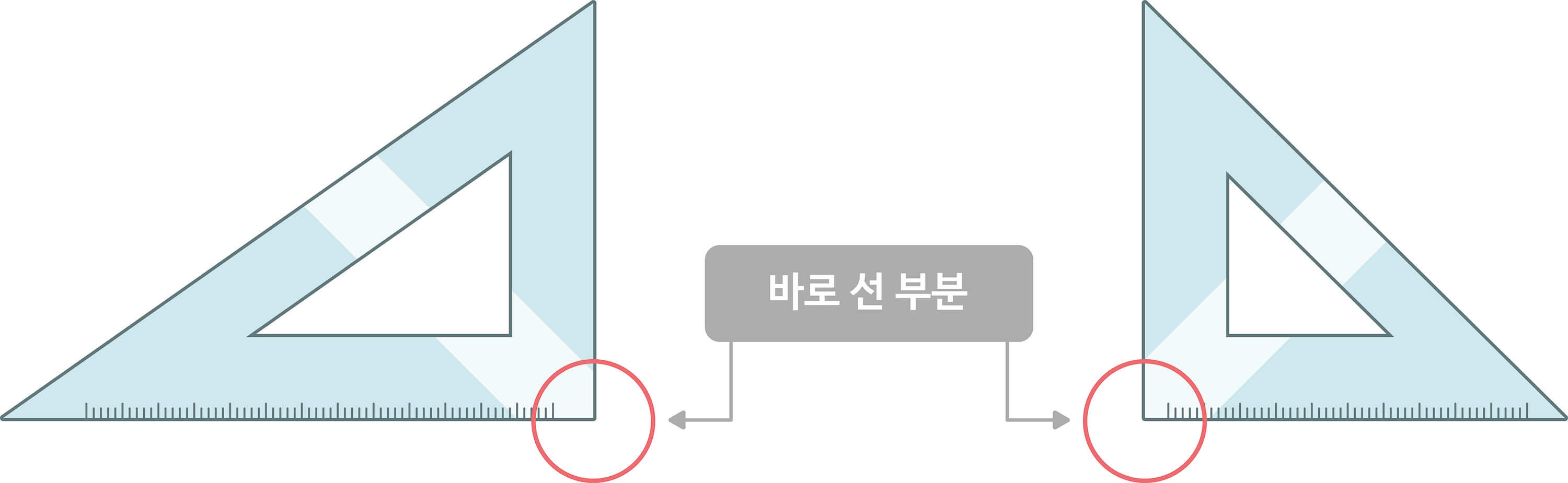
삼각자의 바로 선 부분이 있는 삼각형을 직각삼각형이라고 합니다. (한 내각이 직각인 삼각을 직각삼각형이라고 합니다.)
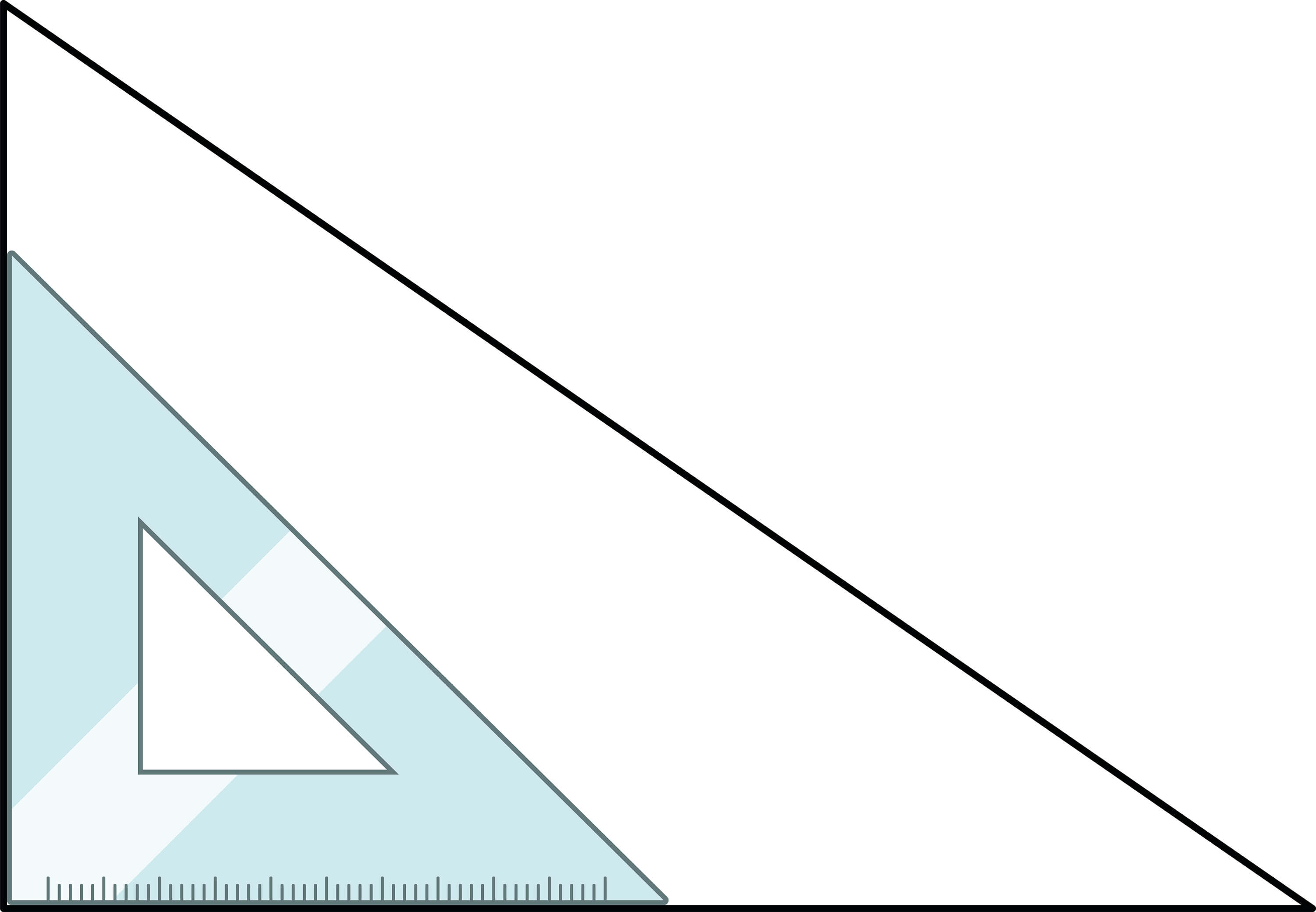
3-1. 예각삼각형에 대해 알기
삼각형의 꼭짓점의 부분이 삼각자의 바로 선 부분보다 작은 부분만 있는 삼각형을 예각삼각형이라고 합니다. (내각이 모두 예각인 삼각형을 예각삼각형이라고 합니다.)
*예각 : 0°보다 크고, 직각(90°)보다 작은 각. 예각은 둔각보다 작은 각이다.
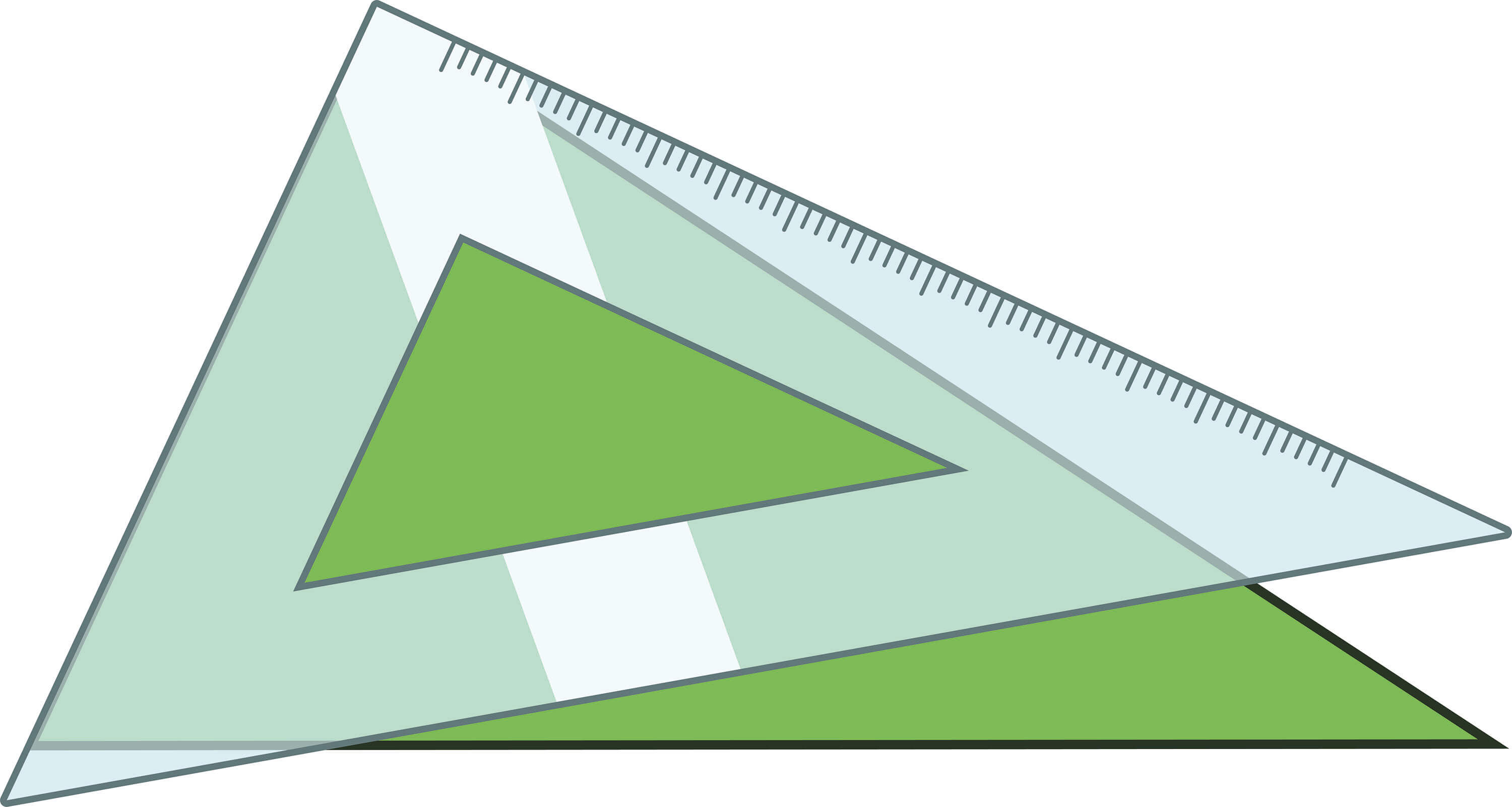
3-2. 둔각삼각형에 대해 알기
삼각형의 꼭짓점의 부분이 삼각자의 바로 선 부분보다 큰 부분이 있는 삼각형을 둔각삼각형이라고 합니다. (세 개의 내각 가운데 하나가 둔각인 삼각형을 둔각삼각형이라고 합니다.)
*둔각 : 직각(90°)보다 크고, 180°보다 작은 각. 180°보다 큰 각은 둔각이 아니다.
1. 정삼각형 그리기
다음과 같이 블록 코딩하여 터틀 로봇과 함께 정삼각형을 그려봅시다.
[활동지 4-1]
[ 블록 코딩 ]
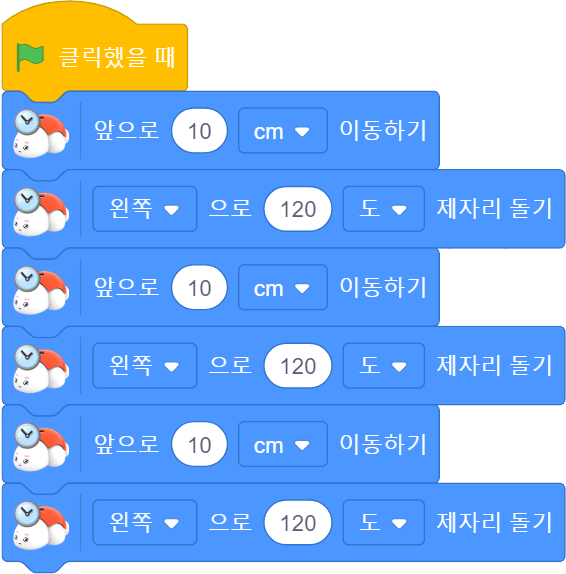
[ 정삼각형 ]


▣ 터틀 로봇과 함께 그린 삼각형을 살펴봅시다. 터틀 로봇과 함께 그린 삼각형의 세 변의 길이는 모두 같습니다. 이렇게 세 변의 길이가 모두 같은 삼각형을 정삼각형이라고 합니다.
2. 이등변삼각형 그리기
다음과 같이 블록 코딩하여 터틀 로봇과 함께 이등변삼각형을 그려봅시다.
[활동지 4-2]
[ 블록 코딩 ]
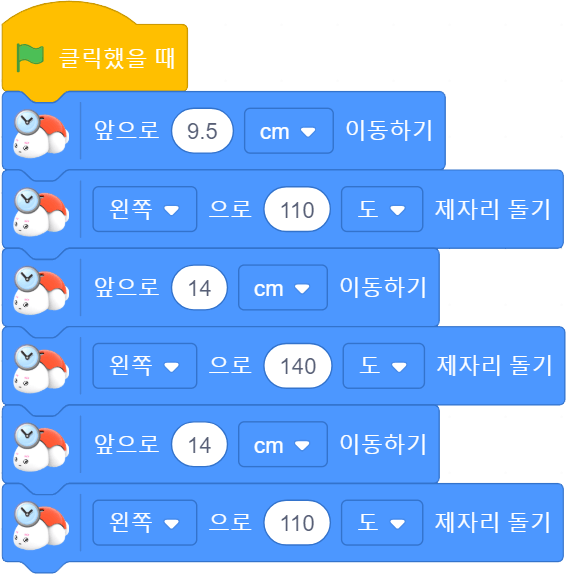
[ 이등변삼각형 ]


▣ 터틀 로봇과 함께 그린 삼각형을 살펴봅시다. 터틀 로봇과 함께 그린 삼각형의 두 변의 길이는 같습니다. 이렇게 세 변의 길이 중 두 변의 길이가 같은 삼각형을 이등변삼각형이라고 합니다.
3. 직각삼각형 그리기
다음과 같이 블록 코딩하여 터틀 로봇과 함께 직각삼각형을 그려봅시다.
[활동지 4-3]
[ 블록 코딩 ]
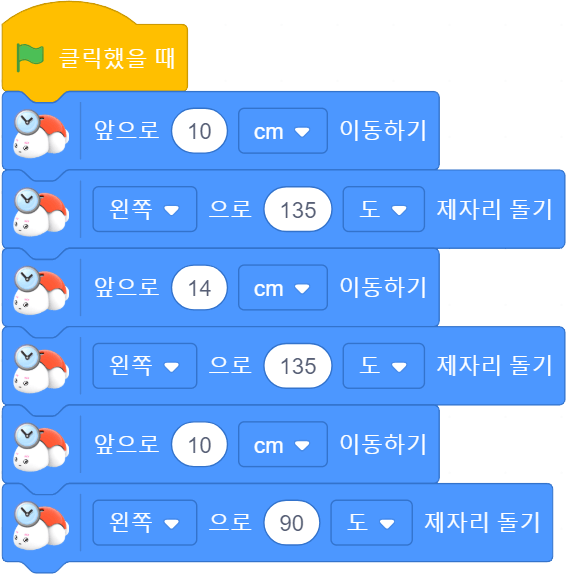
[ 직각삼각형 ]
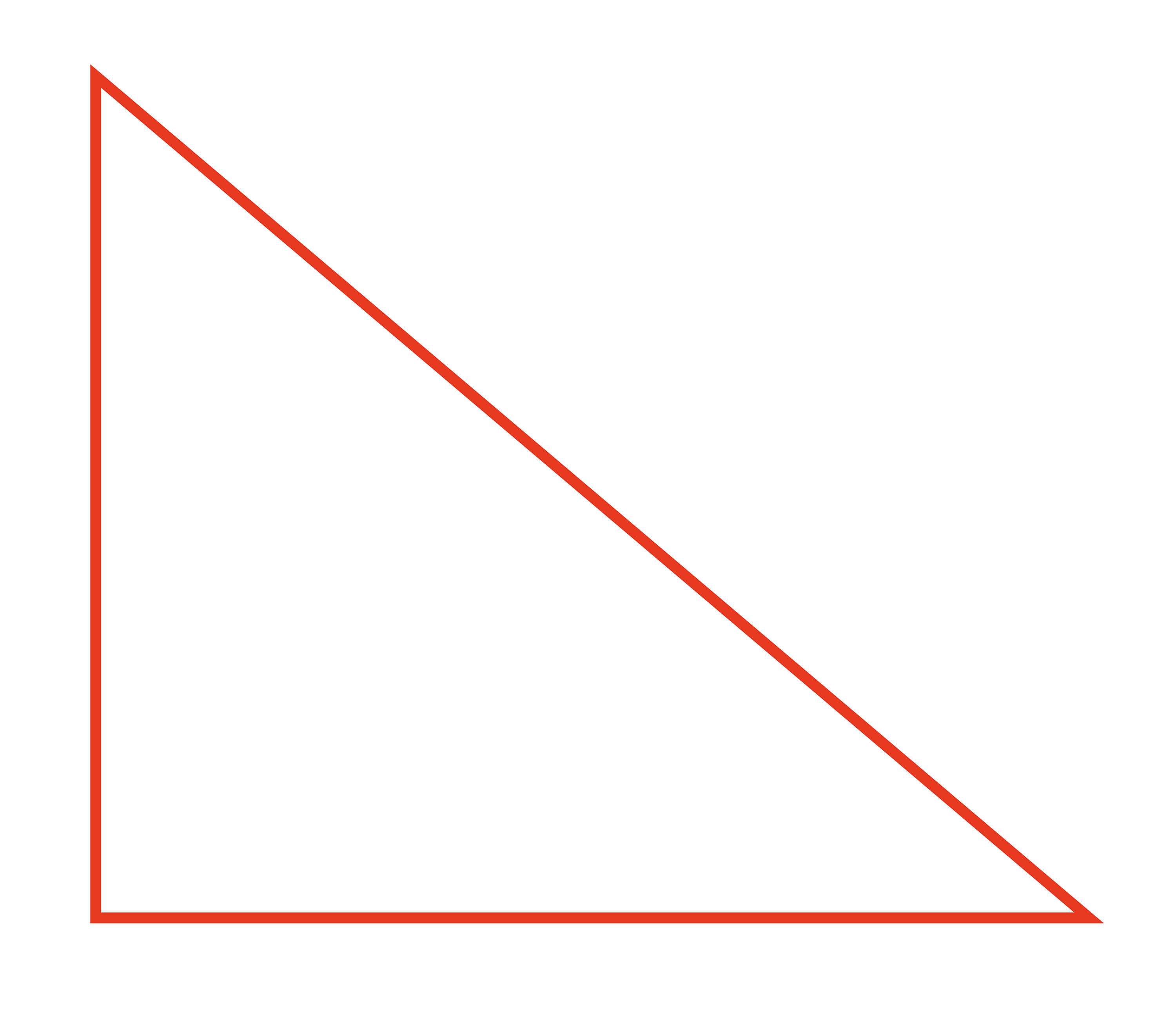

▣ 터틀 로봇과 함께 그린 삼각형을 살펴봅시다. 터틀 로봇과 함께 그린 삼각형에는 삼각자의 바로 선 부분이 있습니다. 이렇게 삼각형에서 바로 선 부분이 있는 삼각형을 직각삼각형이라고 합니다.
1. 예각삼각형 그리기
다음과 같이 블록 코딩하여 터틀 로봇과 함께 예각삼각형을 그려봅시다.
[활동지 4-4]
[ 블록 코딩 ]
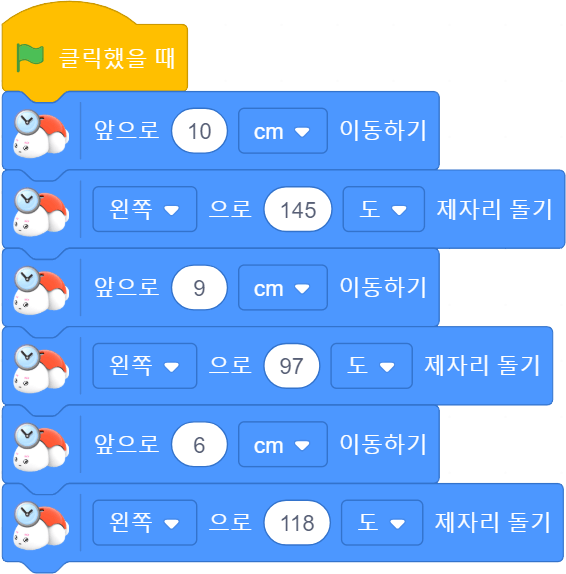
[ 예각삼각형 ]
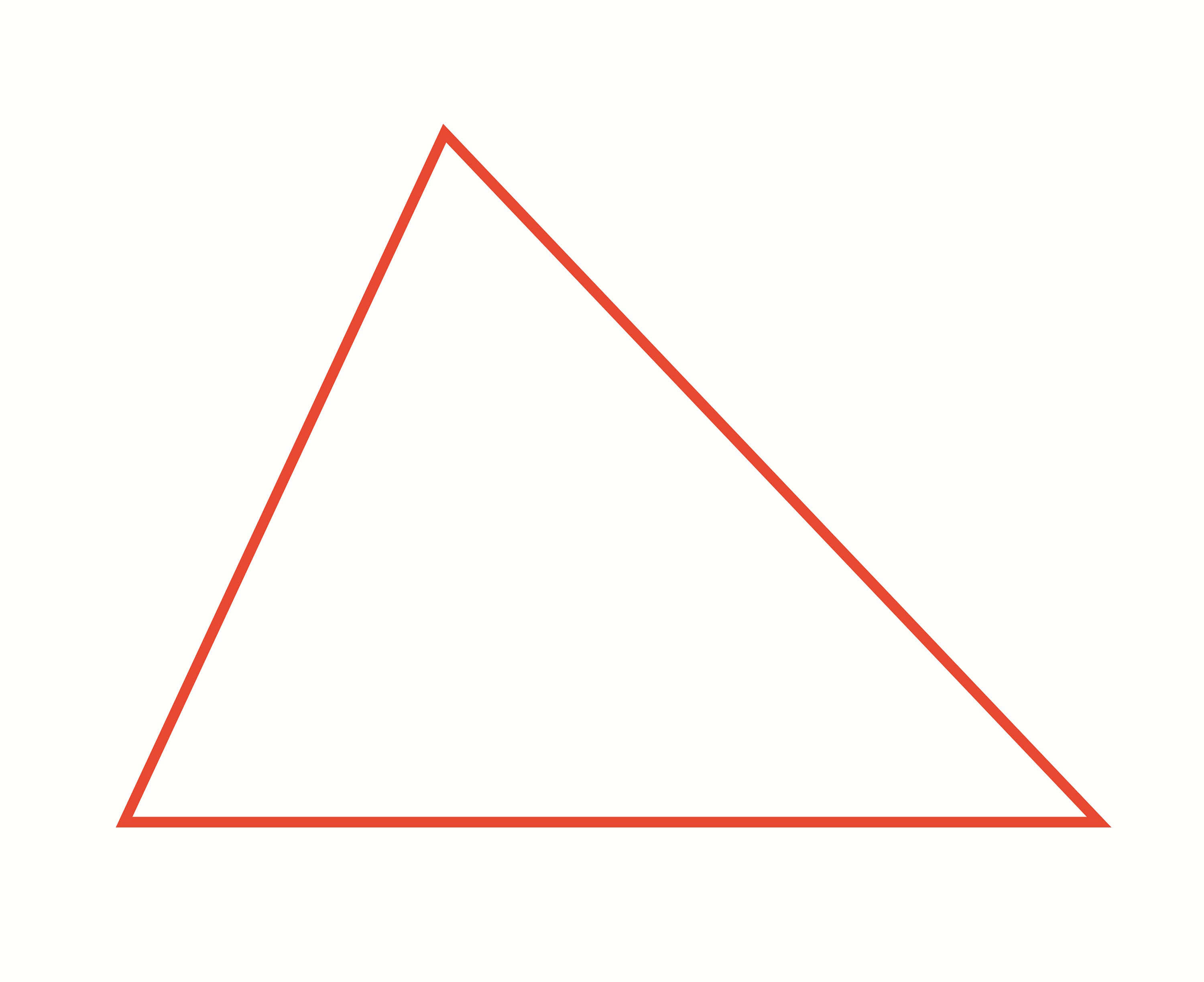

▣ 터틀 로봇과 함께 그린 삼각형을 살펴봅시다. 터틀 로봇과 함께 그린 삼각형의 꼭짓점 부분은 삼각자의 바로 선 부분보다 작은 부분만 있습니다. 이렇게 삼각형의 꼭짓점의 부분이 삼각자의 바로 선 부분보다 작은 부분만 있는 삼각형을 예각 삼각형이라고 합니다.
2. 둔각삼각형 그리기
다음과 같이 블록 코딩하여 터틀 로봇과 함께 둔각삼각형을 그려봅시다.
[활동지 4-5]
[ 블록 코딩 ]
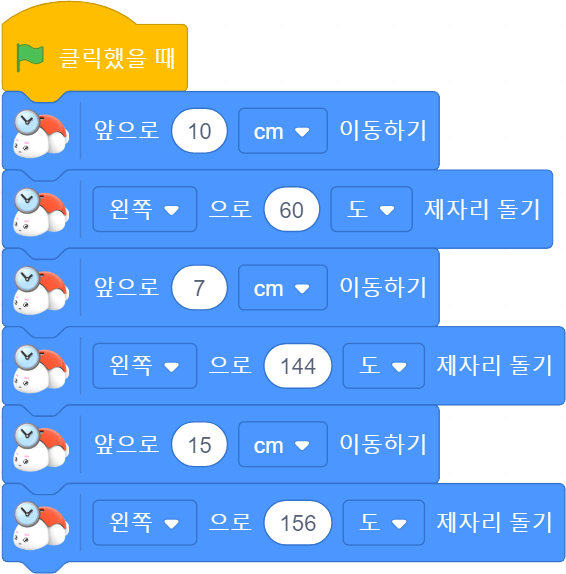
[ 둔각삼각형 ]
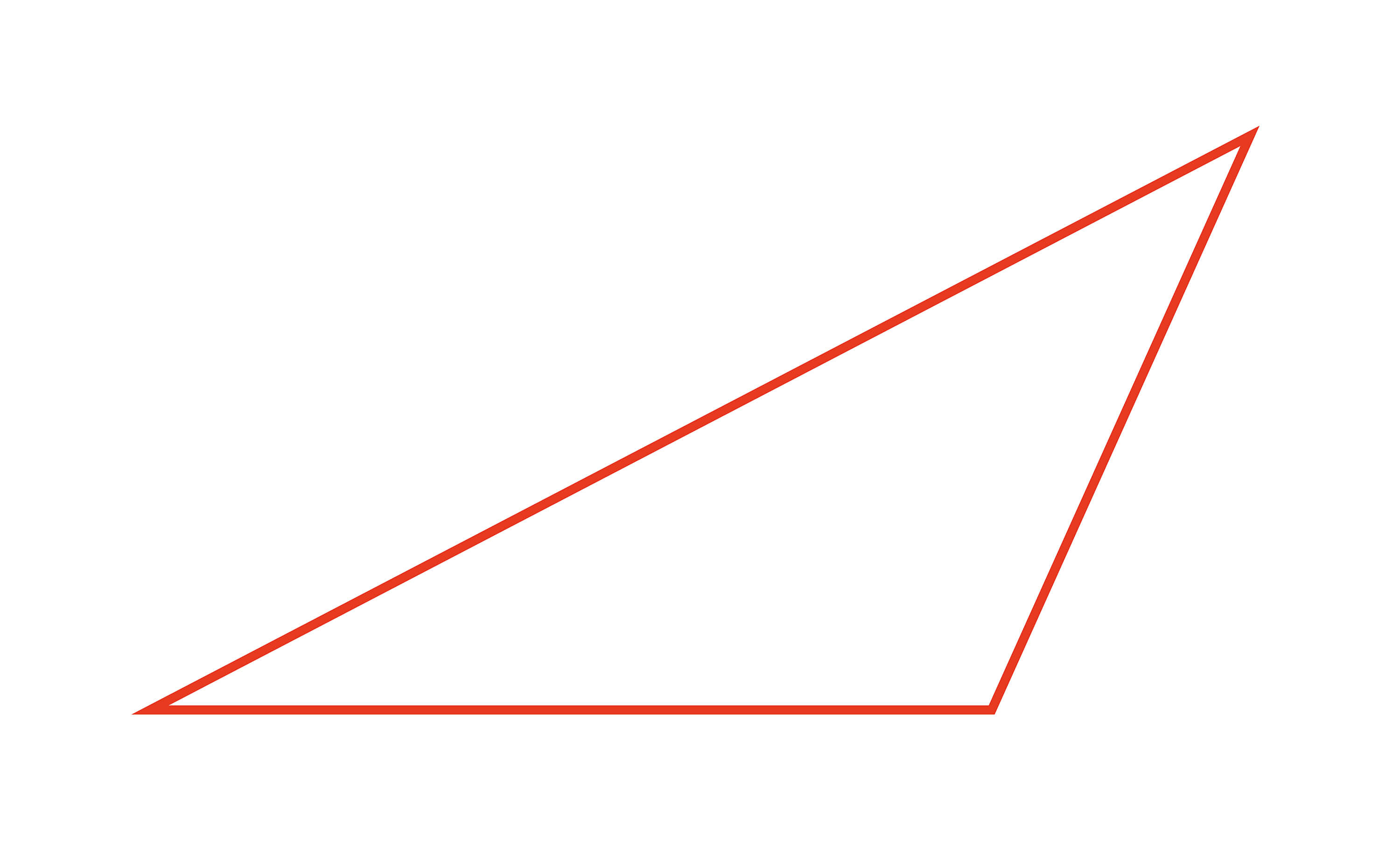

▣ 터틀 로봇과 함께 그린 삼각형을 살펴봅시다. 터틀 로봇과 함께 그린 삼각형의 꼭짓점 부분은 삼각자의 바로 선 부분보다 큰 부분이 있습니다. 이렇게 삼각형의 꼭짓점의 부분이 삼각자의 바로 선 부분보다 큰 부분이 있는 삼각형을 둔각 삼각형이라고 합니다.
여러 가지 삼각형으로 자유롭게 그림을 그려봅시다
[활동지 4-6]
핵심 개념 정리
■ 삼각형의 특징: 삼각형은 변과 꼭짓점의 수가 각각 3개임
■ 블록 코딩: 텍스트를 입력하여 코딩하지 않고 블록을 조합하여 코딩하는 것
함께 확인해요! - 학습활동 평가
| 평가영역 | 평가내용 | 평가결과 |
|---|---|---|
| 지식 | 삼각형의 변과 꼭짓점을 찾고 개수를 셀 수 있는가? | |
| 삼각형의 특징을 알고 있는가? | ||
| 정삼각형, 이등변삼각형, 직각삼각형, 예각삼각형, 둔각삼각형을 구분할 수 있는가? | ||
| 기능 | 블록 코딩을 따라 하여 정삼각형, 이등변 삼각형, 직각삼각형, 예각삼각형, 둔각삼각형을 그릴 수 있는가? | |
| 태도 | 수업활동에 흥미를 가지고 바른 자세로 참여할 수 있는가? |